(·湖南长沙)若关于x的二次函数y=a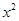 +bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A(
+bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A(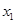 ,0),B(
,0),B(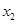 ,0)(0<
,0)(0<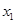 <
<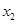 ),与y轴交于点P,其图像顶点为点M,点O为坐标原点。
),与y轴交于点P,其图像顶点为点M,点O为坐标原点。

(1)当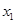 =c=2,a=
=c=2,a=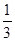 时,求
时,求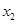 与b的值;
与b的值;
(2)当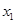 =2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
=2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
(3)当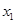 =mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
=mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
|
(·湖南长沙)若关于x的二次函数y=a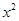 +bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A(
+bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A(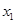 ,0),B(
,0),B(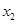 ,0)(0<
,0)(0<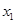 <
<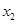 ),与y轴交于点P,其图像顶点为点M,点O为坐标原点。
),与y轴交于点P,其图像顶点为点M,点O为坐标原点。

(1)当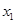 =c=2,a=
=c=2,a=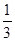 时,求
时,求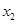 与b的值;
与b的值;
(2)当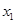 =2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
=2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
(3)当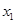 =mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
=mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
|