（南充）如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．
（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）
（2）如果AM=1，sin∠DMF=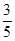
，求AB的长．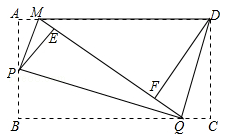
相关试题
（南充）如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．
（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）
（2）如果AM=1，sin∠DMF=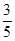，求AB的长．
．
粤公网安备 44130202000953号