如图,已知抛物线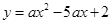 (
(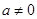 )与y轴交于点C,与x轴交于点A(1,0)和点B.
)与y轴交于点C,与x轴交于点A(1,0)和点B.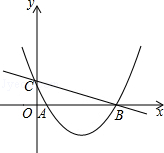
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.
如图,已知抛物线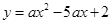 (
(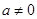 )与y轴交于点C,与x轴交于点A(1,0)和点B.
)与y轴交于点C,与x轴交于点A(1,0)和点B.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.