（自贡）观察下表
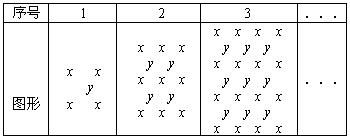
我们把某格中字母和所得的多项式称为特征多项式，例如第1格的“特征多项式”为4x＋y，回答下列问题：
（1）第3格的“特征多项式”为 ，第4格的“特征多项式”为 ，第n格的“特征多项式”为 ；
（2）若第1格的“特征多项式”的值为－10，第2格的“特征多项式”的值为－16，
①求x，y的值；
②在此条件下，第n格的特征是否有最小值？若有，求出最小值和相应的n值，若没有，说明理由．
相关试题
如图，在边长为1的正方形组成的网格中，
的顶点均在格点上，其中点
（5，4），
（1，3），将绕点
逆时针旋转
后得到
．
（1）画出；
（2）在旋转过程中点所经过的路径长为___________.
（3）求在旋转过程中线段
、
扫过的图形的面积之和．
中，
，
平分
交
于点
，点
在
边上且
． 
外接圆的位置关系，并说明理由； 
,
，求
的长．电动自行车已成为市民日常出行的首选工具.据某市品牌电动
自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月销售216辆.
（1）求该品牌电动车销售量的月平均增长率；
（2）若该品牌电动自行车的进价为2300元，售价2800元，则该经销商1月至3月共盈利多少元？
的方程
．
的取值范围；
（配方法）
（公式法）
粤公网安备 44130202000953号