(南充)已知抛物线 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
( )与抛物线相交于两点M(
)与抛物线相交于两点M( ,
, ),N(
),N( ,
, )(
)(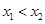 ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.
(南充)已知抛物线 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
( )与抛物线相交于两点M(
)与抛物线相交于两点M( ,
, ),N(
),N( ,
, )(
)(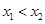 ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.