（本小题满分13分）
在平面直角坐标系中，O为原点，直线y =－2x－1与y轴交于点A，与直线y =－x交于点B, 点B关于原点的对称点为点C．
（1）求过A，B，C三点的抛物线的解析式；
（2）P为抛物线上一点，它关于原点的对称点为Q．
①当四边形PBQC为菱形时，求点P的坐标；
②若点P的横坐标为t（－1＜t＜1），当t为何值时，四边形PBQC面积最大，并说明理由．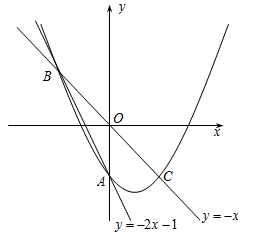
相关试题
（本小题满分13分）
在平面直角坐标系中，O为原点，直线y =－2x－1与y轴交于点A，与直线y =－x交于点B, 点B关于原点的对称点为点C．
（1）求过A，B，C三点的抛物线的解析式；
（2）P为抛物线上一点，它关于原点的对称点为Q．
①当四边形PBQC为菱形时，求点P的坐标；
②若点P的横坐标为t（－1＜t＜1），当t为何值时，四边形PBQC面积最大，并说明理由．
与
轴交于点
，与
轴交于点
．点
在
轴上，且
，在此平面上，存在点
，使得四边形
恰好为平行四边形.
（
）
千米到李庄，甲比乙每小时多走
千米，结果比乙早到半小时.问二人每小时各走几千米？
中，点
在边
上，
为等边三角形，且点
与点
的两侧，点
在
上（不与
重合）且
，
与
分别相交于点
．
是平行四边形
粤公网安备 44130202000953号