（·辽宁锦州）如图，在平面直角坐标系中，抛物线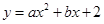
经过点A（﹣1，0）和点B（4，0），且与y轴交于点C，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点，连接CA，CD，PD，PB．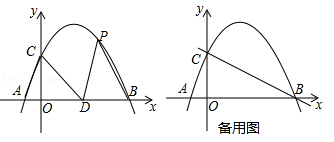
（1）求该抛物线的解析式；
（2）当△PDB的面积等于△CAD的面积时，求点P的坐标；
（3）当m＞0，n＞0时，过点P作直线PE⊥y轴于点E交直线BC于点F，过点F作FG⊥x轴于点G，连接EG，请直接写出随着点P的运动，线段EG的最小值．
（·辽宁锦州）如图，在平面直角坐标系中，抛物线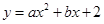经过点A（﹣1，0）和点B（4，0），且与y轴交于点C，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点，连接CA，CD，PD，PB．
（1）求该抛物线的解析式；
（2）当△PDB的面积等于△CAD的面积时，求点P的坐标；
（3）当m＞0，n＞0时，过点P作直线PE⊥y轴于点E交直线BC于点F，过点F作FG⊥x轴于点G，连接EG，请直接写出随着点P的运动，线段EG的最小值．
，其中x=2.
，其中
:（1）有意义?（2）无意义?（3）分式的值为零?
粤公网安备 44130202000953号