如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ．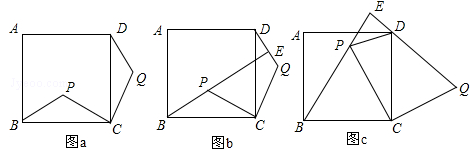
（1）如图a，求证：△BCP≌△DCQ；
（2）如图，延长BP交直线DQ于点E．
①如图b，求证：BE⊥DQ；
②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．
如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ．
（1）如图a，求证：△BCP≌△DCQ；
（2）如图，延长BP交直线DQ于点E．
①如图b，求证：BE⊥DQ；
②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．
；（2）
.
.
的值(1)为正；(2)值为负；(3)值为0.
； (2)
.
粤公网安备 44130202000953号