（年山东临沂13分）如图，在平面直角坐标系中，抛物线与x轴交于点A（﹣1，0）和点B（1，0），直线y=2x﹣1与y轴交于点C，与抛物线交于点C、D．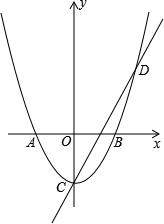
（1）求抛物线的解析式；
（2）求点A到直线CD的距离；
（3）平移抛物线，使抛物线的顶点P在直线CD上，抛物线与直线CD的另一个交点为Q，点G在y轴正半轴上，当以G、P、Q三点为顶点的三角形为等腰直角三角形时，求出所有符合条件的G点的坐标．
相关试题
网格中每个小正方形的边长都是1.
（1）将图①中的格点三角形ABC平移，使点A平移至点A`，画出平移后的三角形；
（2）在图②中画一个格点三角形DEF，使△DEF∽△ABC，且相似比为2∶1；
（3）在图③中画一个格点三角形PQR，使△PQR∽△ABC，且相似比为
∶1.
cm.
的长（结果保留
）.
，求锐角α；
．如图，在直角梯形ABCD中,AD∥CB, 
,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t（秒）.
（1）设△BPQ的面积为S,求S与t之间的函数关系式;
（2）当t为何值时,四边形ABQP是平行四边形.
（3）当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
的解析表达式为
，且
轴交于点
，直线
经过点
，直线
．
的面积。
粤公网安备 44130202000953号