（年四川南充10分）如图，抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点．点A的横坐标为﹣3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D．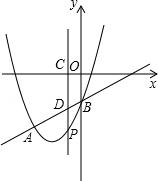
（1）求抛物线的解析式；
（2）当m为何值时，S四边形OBDC=2S△BPD；
（3）是否存在点P，使△PAD是直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
（年四川南充10分）如图，抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点．点A的横坐标为﹣3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D．
（1）求抛物线的解析式；
（2）当m为何值时，S四边形OBDC=2S△BPD；
（3）是否存在点P，使△PAD是直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
中，
是
边上的高，
求
的长．(结果保留根号)
，
分别满足
，
，且
的值。
0
粤公网安备 44130202000953号