如图，将△ABC在网格中（网格中每个小正方形的边长均为1）依次进行位似变换、轴对称变换和平移变换后得到△A1B1C1．
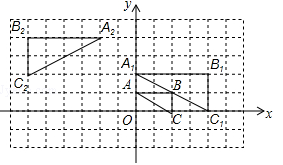
（1）△ABC与△A1B1C1的位似比等于 ；
（2）在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2；
（3）请写出△A1B1C1是由△A2B2C2怎样平移得到的？
（4）设点P（x，y）为△ABC内一点，依次经过上述三次变换后，点P的对应点的坐标为 ．
如图，奥运福娃在5×5的方格（每小格边长为1m）上沿着网格线运动．贝贝从A处出发去寻找B、C、D处的其它福娃，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（＋1，＋4），从B到A记为：B→A（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）B→D（ ， ），,C→ （-3，-4）；
（2）若贝贝从A处去寻找妮妮的行走路线依次为（＋2，＋2），（＋2，－1），（－2，＋3），（－1，－2），请在图中标出妮妮的位置E点．
（3）在（3）中贝贝若每走1m需消耗1．5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
定义一种新运算：观察下列各式：1⊙3=1×4+3=7 ；3⊙（－1）= 3×4－1=11；5⊙4="5×4+4=24" ；4⊙（－3）= 4×4－3=13
（1）请你想一想：用代数式表示a⊙b的结果为：___________；
（2）若a≠b,那么a⊙b______b⊙a（填入“=”或“≠ ”）；
（3）若a⊙（－2b）= 4，请计算（a－b）⊙（2a+b）的值．
新学期，两摞规格相同的数学课本整齐的叠放在课桌上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的厚度为 cm，课桌的高度为 cm；
（2）当课本数为
（本）时，请直接写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含的代数式表示）；
（3）利用（2）中的结论解决问题：桌面上有45本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走15本，求余下的数学课本高出地面的距离．
、
；
．
粤公网安备 44130202000953号