一条东西走向的高速公路上有两个加油站
、
，在的北偏西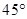
方向还有一个加油站
，到高速公路的最短距离是30千米，、间的距离是60千米．想要经过修一条笔直的公路与高速公路相交，使两路交叉口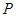
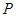到、的距离相等，请求出交叉路口与加油站的距离（结果保留根号）．
，则
=______________.
，则
_______.
，则
的值为_______.
，定义一种运算“
”如下：
.那么
_______.
、
均被直线
、
所截，且
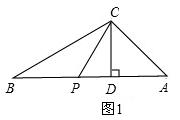
相关知识点
推荐套卷
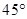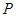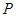一条东西走向的高速公路上有两个加油站、，在的北偏西方向还有一个加油站，到高速公路的最短距离是30千米，、间的距离是60千米．想要经过修一条笔直的公路与高速公路相交，使两路交叉口到、的距离相等，请求出交叉路口与加油站的距离（结果保留根号）．
粤公网安备 44130202000953号