（·辽宁丹东）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．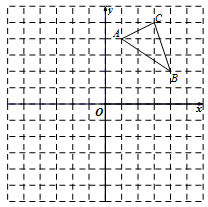
（1）请画出△A1B1C1，使△A1B1C1与△ABC关于x轴对称；
（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点B旋转到点B2所经过的路径长．
相关试题
如图，直线DE和BC被直线AB所截．
(1)∠1与∠2，∠1与∠3，∠1与∠4各是什么角？
(2)∠1与∠5是内错角吗？
(3)如果∠1＋∠3＝180°，那么∠1等于∠2吗？∠1和∠5互补吗？为什么？
粤公网安备 44130202000953号