(·辽宁丹东)如图,已知二次函数y= ax2+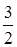 x+c 的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c 的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y= ax2+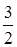 x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
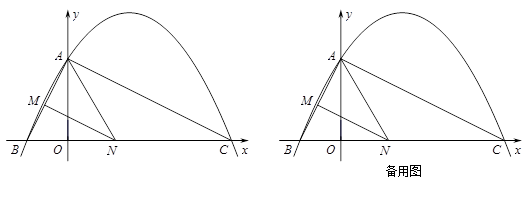
(·辽宁丹东)如图,已知二次函数y= ax2+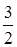 x+c 的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c 的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y= ax2+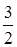 x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
