（·辽宁大连）如图，在平面坐标系中，∠AOB=90°，AB∥x轴，OB=2，双曲线y=
经过点B．将△AOB绕点B逆时针旋转，使点O的对应点D落在X轴的正半轴上．若AB的对应线段CB恰好经过点O．
（1）点B的坐标和双曲线的解析式．
（2）判断点C是否在双曲线上，并说明理由．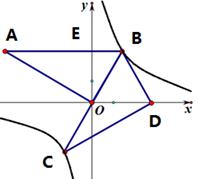
（·辽宁大连）如图，在平面坐标系中，∠AOB=90°，AB∥x轴，OB=2，双曲线y=经过点B．将△AOB绕点B逆时针旋转，使点O的对应点D落在X轴的正半轴上．若AB的对应线段CB恰好经过点O．
（1）点B的坐标和双曲线的解析式．
（2）判断点C是否在双曲线上，并说明理由．
．
．
．（2）解方程
=0．
．
粤公网安备 44130202000953号