(本小题9分)如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y= +bx+c的图象经过B、C两点.
+bx+c的图象经过B、C两点.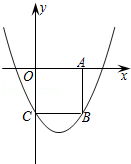
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时,x的取值范围.
相关知识点
推荐套卷
(本小题9分)如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y= +bx+c的图象经过B、C两点.
+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时,x的取值范围.