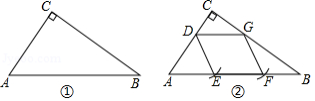
如图①，在 中， ， ， ．求作菱形 ，使点 在边 上，点 、 在边 上，点 在边 上．
小明的作法
1．如图②，在边 上取一点 ，过点 作 交 于点 ．
2．以点 为圆心， 长为半径画弧，交 于点 ．
3．在 上截取 ，连接 ，则四边形 为所求作的菱形．
（1）证明小明所作的四边形 是菱形．
（2）小明进一步探索，发现可作出的菱形的个数随着点 的位置变化而变化 请你继续探索，直接写出菱形的个数及对应的 的长的取值范围．
小华观察钟面（图（1）），了解到钟面上的分针每小时旋转 度，时针每小时旋转 度．他为了进一步研究钟面上分针与时针的旋转规律，从下午 开始对钟面进行了一个小时的观察，为了方便，他将分针与时针原始位置 （图（2））的夹角记为 度，时针与原始位置 的夹角记为 度，（夹角是指不大于平角的角），旋转时间为 ，观察结束后，他利用所得的数据制成图象（图（3）），并求出 与 的函数关系式
请你完成：
（1）求出题图（3）中 与 的函数关系式；
（2）直接写出 两点的坐标，并解释这两点的实际意义；
（3）若小华继续观察一小时，请你在图（3）中补全图象．
市， 市和 市分别有某种机器 台， 台和 台。现决定把这些机器支援给 市 台， 市 台。已知从 市调运一台机器到 市， 市的运费分别为 元和 元；从 市调运一台机器到 市， 市的运费分别为 元和 元；从 市调运一台机器到 市， 市的运费分别为 元和 元．
（1）设从 市， 市各调运 台机器到 市，当 台机器全部调运完毕后，求总运费 （元）关于 （台）的函数式，并求 的最小值和最大值；
（2）设从 市调 台到 市， 市调 台到 市，当 台机器全部调运完毕后，用 表示总运费 （元），并求 的最小值和最大值．
某商业集团新进了 台空调， 台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中 台给甲连锁店， 台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：
设集团调配给甲连锁店 台空调，集团卖出这 台电器的总利润为 （元）。
（1）写出 关于 的函数解析式，并求出 的取值范围；
（2）为了促销，集团决定仅对甲连锁店的空调每台让利 元销售，其他的销售利润不变，并且让利后每台空调的利润仍然高于甲连锁店销售的每台冰箱的利润，问该集团应该如何设计调配方案，使总利润达到最大?
有一个附有进、出水管的容器，每单位时间内进、出的水量都是一定的，设从某时开始 钟内只进水不出水，在随后的 内既进水又出水，得到时间 与水量 之间的关系如图所示，若 后只出水不进水，求这时（即 ) 与 之间的函数关系式，并求出多长时间可将容器内的水放完?
粤公网安备 44130202000953号