如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°,以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;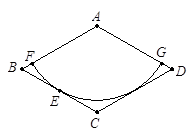
(1)请你判断所作的扇形与边CD的位置关系,并说明理由;
(2)若以所作出的扇形为侧面围成一个圆锥,求该圆锥的全面积.
相关知识点
推荐套卷
如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°,以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;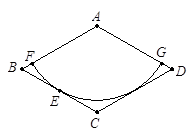
(1)请你判断所作的扇形与边CD的位置关系,并说明理由;
(2)若以所作出的扇形为侧面围成一个圆锥,求该圆锥的全面积.