已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,点M在椭圆上且位于第一象限,直线FM被圆
,点M在椭圆上且位于第一象限,直线FM被圆 截得的线段的长为c,
截得的线段的长为c,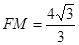 .
.
(Ⅰ)求直线FM的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设椭圆上动点P在x轴上方,若直线FP的斜率大于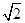 ,求直线OP(O为原点)的斜率的取值范围.
,求直线OP(O为原点)的斜率的取值范围.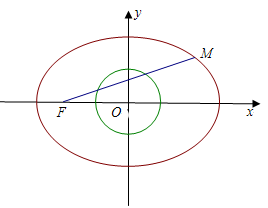
推荐套卷
已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,点M在椭圆上且位于第一象限,直线FM被圆
,点M在椭圆上且位于第一象限,直线FM被圆 截得的线段的长为c,
截得的线段的长为c,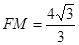 .
.
(Ⅰ)求直线FM的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设椭圆上动点P在x轴上方,若直线FP的斜率大于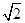 ,求直线OP(O为原点)的斜率的取值范围.
,求直线OP(O为原点)的斜率的取值范围.