（本小题满分12分）设椭圆C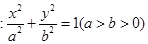
的离心率为
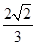，其焦距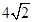
．
（1）求椭圆C的方程；
（2）若P在椭圆上，F1，F2分别为椭圆的左右焦点，且满足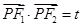
，求实数t的范围；
（3）过点Q（1，0）作直线l （不与x轴垂直）与该椭圆交于M，N两点，与y轴交于点R，若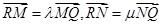
，试判断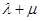
是否为定值，并说明理由．
相关试题
平面
，四边形
为矩形，△
为
的中点，
．
；
的正切值．
中，已知
，
. 
；
，设数列
的前
项和为
，试比较
与
的大小．
中，内角
，
，
的对边分别为
，
，
，且
.
，
，求
，函数
．
时，求
在
内的极大值；
，当
有两个极值点
时，总有
，求实数
的值.（其中
是
的导函数．）
在点
，
处的切线垂直相交于点
，直线
与椭圆
相交于
，
两点．
的焦点
与椭圆
的左焦点
的距离；
，试问：是否存在直线
，
成等比数列？若存在，求直线推荐套卷
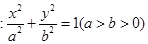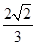（本小题满分12分）设椭圆C 的离心率为，其焦距．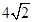
（1）求椭圆C的方程；
（2）若P在椭圆上，F1，F2分别为椭圆的左右焦点，且满足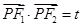，求实数t的范围；
（3）过点Q（1，0）作直线l （不与x轴垂直）与该椭圆交于M，N两点，与y轴交于点R，若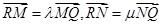，试判断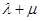是否为定值，并说明理由．
粤公网安备 44130202000953号