设二次函数f（x）=ax2+bx+c（a＞0），方程f（x）﹣x=0的两个根x1，x2满足：0＜x1＜x2＜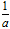
．
（1）当x∈（0， x1）时，证明x＜f（x）＜x1；
（2）设函数f（x）的图象关于直线x=x0对称，证明x0＜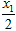
．
推荐套卷
设二次函数f（x）=ax2+bx+c（a＞0），方程f（x）﹣x=0的两个根x1，x2满足：0＜x1＜x2＜．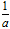
（1）当x∈（0， x1）时，证明x＜f（x）＜x1；
（2）设函数f（x）的图象关于直线x=x0对称，证明x0＜．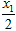
粤公网安备 44130202000953号