(本小题满分11分)
如图，已知点O(0，0)，A(－5，0)，B(2，1)，抛物线l：y＝－(x－h)2＋1(h为常数)与y轴的交点为C.
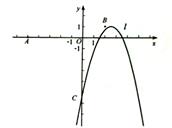
(1)l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标：
(2)设点C的级坐标为yc，求yc的最大值，此时l上有两点(x1，y1)，(x2，y2)，其中x1＞x2≥0，比较y1与y1的大小；
(3)当线段OA被l只分为两部分，且这两部分的比是1:4时，求h的值.
(本小题满分11分)
如图，已知点O(0，0)，A(－5，0)，B(2，1)，抛物线l：y＝－(x－h)2＋1(h为常数)与y轴的交点为C.
(1)l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标：
(2)设点C的级坐标为yc，求yc的最大值，此时l上有两点(x1，y1)，(x2，y2)，其中x1＞x2≥0，比较y1与y1的大小；
(3)当线段OA被l只分为两部分，且这两部分的比是1:4时，求h的值.
x－mx＝5的解，求代数式
的值.
的方程组
的解满足
，求p的取值范围.
≤
的非负整数解.
＞－2
粤公网安备 44130202000953号