(本题6分)在3×3的正方形网格中,有一个以格点为顶点的三角形(阴影部分)如图所示,请你在图①,图②,图③中,分别画出一个与该三角形成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)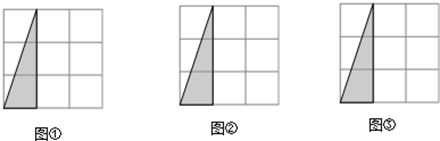
相关知识点
推荐套卷
(本题6分)在3×3的正方形网格中,有一个以格点为顶点的三角形(阴影部分)如图所示,请你在图①,图②,图③中,分别画出一个与该三角形成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)