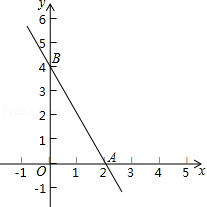如果两个一次函数 和 满足 , ,那么称这两个一次函数为“平行一次函数”.
如图,已知函数 的图象与 轴、 轴分别交于 、 两点,一次函数 与 是“平行一次函数”
(1)若函数 的图象过点 ,求 的值;
(2)若函数 的图象与两坐标轴围成的三角形和 构成位似图形,位似中心为原点,位似比为 ,求函数 的表达式.
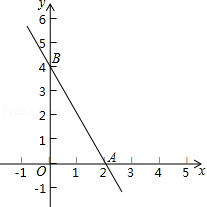
相关知识点
推荐套卷
如果两个一次函数 和 满足 , ,那么称这两个一次函数为“平行一次函数”.
如图,已知函数 的图象与 轴、 轴分别交于 、 两点,一次函数 与 是“平行一次函数”
(1)若函数 的图象过点 ,求 的值;
(2)若函数 的图象与两坐标轴围成的三角形和 构成位似图形,位似中心为原点,位似比为 ,求函数 的表达式.