(本小题满分16分)已知直线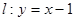 与⊙
与⊙ 相交于A,B两点,过点A,B的两条切线相交于点P.
相交于A,B两点,过点A,B的两条切线相交于点P.
(1)求点P的坐标;
(2)若N为线段AB上的任意一点(不包括端点),过点N的直线交⊙O于C,D两点,过点C、D的两条切线相交于点Q,判断点Q的轨迹是否经过定点?若过定点,求出该点的坐标;若不过定点,说明理由.
相关知识点
推荐套卷
(本小题满分16分)已知直线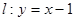 与⊙
与⊙ 相交于A,B两点,过点A,B的两条切线相交于点P.
相交于A,B两点,过点A,B的两条切线相交于点P.
(1)求点P的坐标;
(2)若N为线段AB上的任意一点(不包括端点),过点N的直线交⊙O于C,D两点,过点C、D的两条切线相交于点Q,判断点Q的轨迹是否经过定点?若过定点,求出该点的坐标;若不过定点,说明理由.