（本题14分）如图所示，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80 m．经测量，点A位于点O正北方向60 m处，点C位于点O正东方向170 m处（OC为河岸），tan∠BCO＝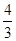
．
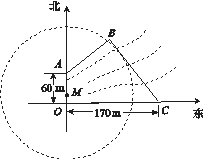
（1）求新桥BC的长．
（2）当OM多长时，圆形保护区的面积最大？
相关试题
是奇函数，且
.
的值；
在
上的单调性，并用定义加以证明．
，
，
．
，求
，(∁
)
；
，求实数
的取值范围.
过点（0，4），离心率为
的直线被C所截线段的长度.
时，求k的值.
为坐标原点，如果一个椭圆经过点P(3,
),且以点F(2,0)为它的一个焦点.推荐套卷
（本题14分）如图所示，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80 m．经测量，点A位于点O正北方向60 m处，点C位于点O正东方向170 m处（OC为河岸），tan∠BCO＝．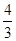
（1）求新桥BC的长．
（2）当OM多长时，圆形保护区的面积最大？
粤公网安备 44130202000953号