附加题
把几个数用大括号围起来,各数中间用逗号隔开,如:{1,2,-3}、
{−2,7, 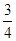 ,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
(1)请你判断集合{1,2},{-2,1,2.5,4,7}是不是“好集合”?
(2)请你再写出两个“好集合”(不得与上面出现过的集合重复).
(3)写出所有“好集合”中,元素个数最少的集合.
附加题
把几个数用大括号围起来,各数中间用逗号隔开,如:{1,2,-3}、
{−2,7, 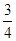 ,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
(1)请你判断集合{1,2},{-2,1,2.5,4,7}是不是“好集合”?
(2)请你再写出两个“好集合”(不得与上面出现过的集合重复).
(3)写出所有“好集合”中,元素个数最少的集合.