（本小题满分12分）为了了解中学生的体能状况，某校抽取了n名高一学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中第二小组频数为14．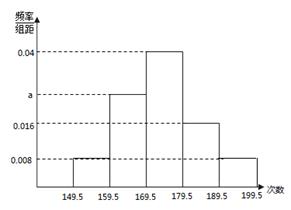
（1）求频率分布直方图中a的值及抽取的学生人数n；
（2）现从跳绳次数在［179．5，199．5］内的学生中随机选取3人，记3人中跳绳次数在［189．5，199．5］内的人数为X，求X的分布列和数学期望．
。
是空集，求
的取值范围；（2）若
，
，
，全集为实数集R。（1）求
，
；（2）若
，求
的取值范围。
，若
，
，求实数
、
的值。
。求证：
推荐套卷
（本小题满分12分）为了了解中学生的体能状况，某校抽取了n名高一学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中第二小组频数为14．
（1）求频率分布直方图中a的值及抽取的学生人数n；
（2）现从跳绳次数在［179．5，199．5］内的学生中随机选取3人，记3人中跳绳次数在［189．5，199．5］内的人数为X，求X的分布列和数学期望．
粤公网安备 44130202000953号