已知圆A：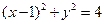
与x轴负半轴交于B点，过B的弦BE与y轴正半轴交于D点，且2BD=DE，曲线C是以A，B为焦点且过D点的椭圆．
（1）求椭圆的方程；
（2）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．
相关试题
(a＞1),判断f(x)=0的根的个数.
-3.相关知识点
推荐套卷
已知圆A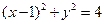：与x轴负半轴交于B点，过B的弦BE与y轴正半轴交于D点，且2BD=DE，曲线C是以A，B为焦点且过D点的椭圆．
（1）求椭圆的方程；
（2）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．
粤公网安备 44130202000953号