如图1，△ABC中，CD⊥AB于D，且BD ：AD ：CD＝2 ：3 ：4．
（1）试说明△ABC是等腰三角形；
（2）已知S△ABC＝40cm2，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒）．
①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．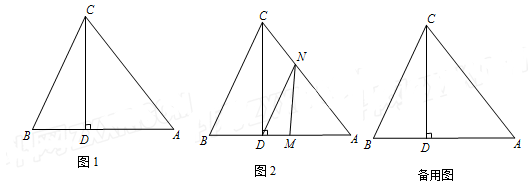
相关试题
无解，求a的取值范围
（2）
（3）
（5）
如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，
求：（1）△ABC的面积；
（2）CD的长；
（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；
（4）作出△BCD的边BC边上的高DF，当BD="11cm" 时，试求出DF的长。
相关知识点
推荐套卷
粤公网安备 44130202000953号