把两个全等的直角三角板ABC和EFG叠放在一起,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF的长均为4。
(1)当EG⊥AC于点K,GF⊥BC于点H时,如图23-1,求GH:GK的值.
(2)现将三角板EFG由图23-1所示的位置绕O点沿逆时针方向旋转,旋转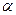 角满足条件:
角满足条件:
0°<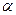 <30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.
<30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.

相关知识点
推荐套卷
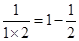
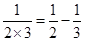
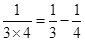 ┅┅
┅┅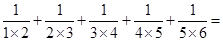 .
.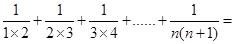 .(用含有
.(用含有 的式子表示)
的式子表示)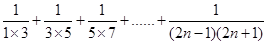 的值为
的值为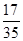 ,求
,求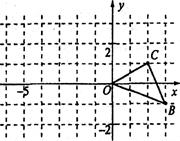
 粤公网安备 44130202000953号
粤公网安备 44130202000953号