由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB = 1米,BC = 5米,两棵树的株距(两棵树的水平距离)为3米,在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?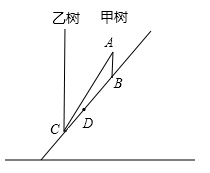
相关知识点
推荐套卷
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB = 1米,BC = 5米,两棵树的株距(两棵树的水平距离)为3米,在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?