（本小题满分12分）已知函数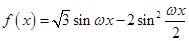
（
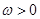）的最小正周期为
．
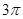（1）求函数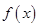
在区间
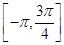上的最大值和最小值；
（2）在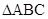
中，
，
，
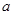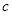分别为角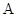
，
，
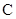所对的边，且
，
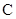，求角的大小；
（3）在（2）的条件下，若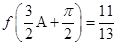
，求
的值．
为定义在
上的奇函数，当
时，
是增函数（2）求
，求
的值。
}，B＝{
}，求
的取值范围．
； （2）已知
求
的值相关知识点
推荐套卷
（本小题满分12分）已知函数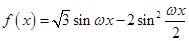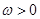（）的最小正周期为．
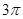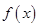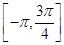（1）求函数在区间上的最大值和最小值；
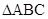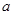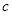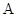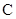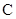（2）在中，，，分别为角，，所对的边，且，，求角的大小；
（3）在（2）的条件下，若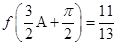，求的值．
粤公网安备 44130202000953号