如果有穷数列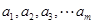
（
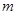为正整数）满足条件
,
,…,
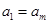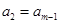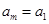,即
（
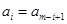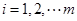）,我们称其为“对称数列”．例如，数列1，2，5，2，1与数列8，4，2，2，4，8都是“对称数列”．
（1）设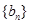
是7项的“对称数列”，其中
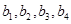是等差数列，且
,
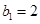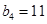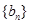．依次写出的每一项；
（2）设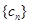
是49项的“对称数列”，其中
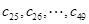是首项为1，公比为2的等比数列，求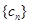各项的和S．
推荐套卷
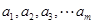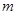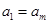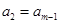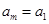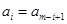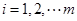如果有穷数列（为正整数）满足条件,,…,,即 （）,我们称其为“对称数列”．例如，数列1，2，5，2，1与数列8，4，2，2，4，8都是“对称数列”．
（1）设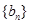是7项的“对称数列”，其中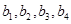是等差数列，且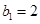,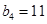．依次写出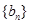的每一项；
（2）设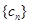是49项的“对称数列”，其中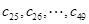是首项为1，公比为2的等比数列，求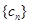各项的和S．
粤公网安备 44130202000953号