观察下列等式：
①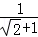
=
=
；
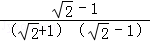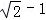②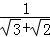
=
=
；
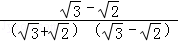③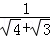
=
=
﹣
；…
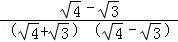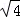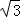回答下列问题：
（1）化简：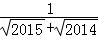
= ；
（2）化简：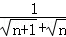
= ；（n为正整数）；
（3）利用上面所揭示的规律计算：
+…+
+
．
的两组解是
和
和
有相同解，求
的值。
并将解集在数轴上表示出来.
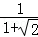
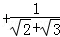
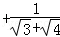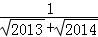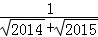相关知识点
推荐套卷
观察下列等式：
①==；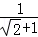
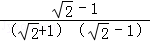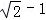②==；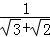
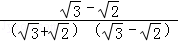③==﹣；…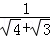
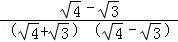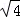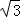回答下列问题：
（1）化简：= ；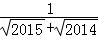
（2）化简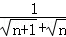：= ；（n为正整数）；
（3）利用上面所揭示的规律计算：
+…++．
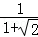
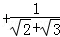
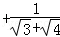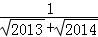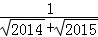粤公网安备 44130202000953号