已知向量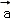
=（
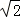cosωx，1），
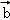=（2sin（ωx+
），﹣1）（其中
≤ω≤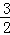
），
函数f（x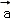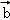）=•，且f（x）图象的一条对称轴为x=
．
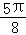（1）求f（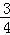
π）的值；
（2）若f（
）=
，f（
﹣
）=
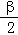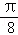，且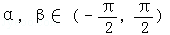
，
求cos（α﹣β）的值．
推荐套卷
已知向量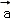=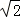（cosωx，1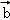），=（2sin（ωx+），﹣1）（其中≤ω≤），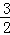
函数f（x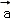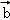）=•，且f（x）图象的一条对称轴为x=．
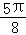（1）求f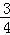（π）的值；
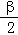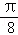（2）若f（）=，f（﹣）=，且，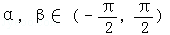
求cos（α﹣β）的值．
粤公网安备 44130202000953号