（本小题满分10分）【选修4一1：几何证明选讲】
如图，已知圆的两条弦AB，CD，延长AB，CD交于圆外一点E，过E作AD的平行线交CB的延长线于F，过点F作圆的切线FG，G为切点．求证：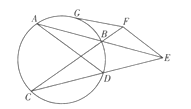
（1）△EFC∽△BFE；
（2）FG＝FE．
相关试题
，
，
, 
，求
及
；
，当
为何值时，
有最小值，最小值是多少？
的值.
，且
时，求：函数
的值；
时，求：函数
上的图象.
、
、
，其中
与
的夹角为
,
的夹角为
,
，并且
的值.
=2，求：
的值；（2）
的值．
满分14分）
的图象在
上连续不断，定义：
，
表示函数
上的最小值，
表示函数
上的最大值．若存在最小正整数
，使得
对任意的
成立，则称函数
收缩函数”．
，
，试写出
，
的表达式；
，
，试判断
上的“
，函数
是
上的2阶收缩函数，求
的取值范围.推荐套卷
（本小题满分10分）【选修4一1：几何证明选讲】
如图，已知圆的两条弦AB，CD，延长AB，CD交于圆外一点E，过E作AD的平行线交CB的延长线于F，过点F作圆的切线FG，G为切点．求证：
（1）△EFC∽△BFE；
（2）FG＝FE．
粤公网安备 44130202000953号