如图，在Rt△ACB中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动，它们的速度都是1米/秒，问：几秒后△PCQ的面积为Rt△ACB面积的一半？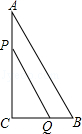
，0
－
×[2－（－3）
]
－
－
）÷（－
）
－
）÷1
÷
相关知识点
推荐套卷
粤ICP备20024846号
粤公网安备 44130202000953号
粤公网安备 44130202000953号
Copyright ©2020-2024 优题课 youtike.com 版权所有
Powered by：Youtike Platform 6.6.2
声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或 联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或 联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。