【选修4-1：几何证明选讲】
如图，在△ABC中，∠ABC=90°，以AB为直径的圆O交AC于点E，点D是BC边上的中点，连接OD交圆O与点M．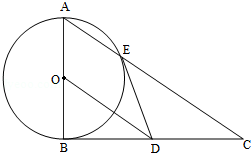
（1）求证：DE是圆O的切线；
（2）求证：DE•BC=DM•AC+DM•AB．
相关知识点
推荐套卷
【选修4-1：几何证明选讲】
如图，在△ABC中，∠ABC=90°，以AB为直径的圆O交AC于点E，点D是BC边上的中点，连接OD交圆O与点M．
（1）求证：DE是圆O的切线；
（2）求证：DE•BC=DM•AC+DM•AB．
粤公网安备 44130202000953号