(绵阳)如图,在边长为2的正方形ABCD中,G是AD延长线时的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
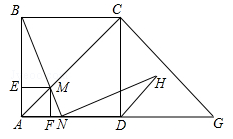
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.