（本小题满分12分）已知函数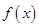
=（sinωx+cosωx）2+
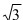（sin2ωx−cos2ωx）,（ω>0）的最小正周期为π。
（1）求ω的值及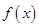的单调递增区间；
（2）在锐角ΔABC中，角ABC所对的边分别为abc，f （A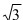）= +1，a=2，且b+c=4，求ΔABC的面积．
相关试题
中，角
所对的边分别为
、
、
．若
＝
，
＝
，且
．
，三角形面积
＝
，求
的值．
的底面为平行四边形，
平面
，
为
中点．
平面
；
，求证：
平面
．
中满足
，
．
和公差
；
．
；
在
上恒成立，求实数
的取值范围．
底面是直角梯形,
底面
,
为
的中点, 
；
；
的体积
．相关知识点
推荐套卷
（本小题满分12分）已知函数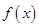=（sinωx+cosωx）2+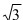（sin2ωx−cos2ωx）,（ω>0）的最小正周期为π。
（1）求ω的值及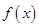的单调递增区间；
（2）在锐角ΔABC中，角ABC所对的边分别为abc，f （A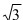）= +1，a=2，且b+c=4，求ΔABC的面积．
粤公网安备 44130202000953号