如图,已知抛物线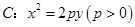 ,其焦点
,其焦点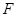 到准线的距离为
到准线的距离为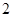 ,点
,点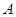 、点
、点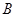 是抛物线
是抛物线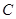 上的定点,它们到焦点
上的定点,它们到焦点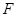 的距离均为
的距离均为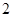 ,且点
,且点 位于第一象限.
位于第一象限.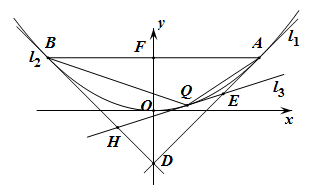
(1)求抛物线 的方程及点
的方程及点 、点
、点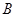 的坐标;
的坐标;
(2)若点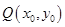 是抛物线
是抛物线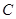 异于
异于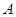 、
、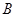 的一动点,分别以点
的一动点,分别以点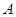 、
、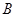 、
、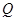 为切点作抛物线
为切点作抛物线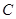 的三条切线
的三条切线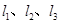 ,若
,若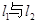 、
、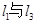 、
、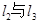 分别相交于D、E、H,设
分别相交于D、E、H,设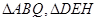 的面积依次为
的面积依次为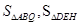 ,记
,记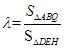 ,问:
,问: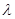 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
相关知识点
推荐套卷
如图,已知抛物线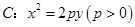 ,其焦点
,其焦点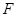 到准线的距离为
到准线的距离为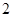 ,点
,点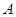 、点
、点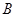 是抛物线
是抛物线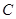 上的定点,它们到焦点
上的定点,它们到焦点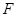 的距离均为
的距离均为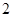 ,且点
,且点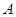 位于第一象限.
位于第一象限.
(1)求抛物线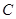 的方程及点
的方程及点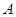 、点
、点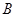 的坐标;
的坐标;
(2)若点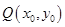 是抛物线
是抛物线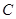 异于
异于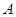 、
、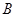 的一动点,分别以点
的一动点,分别以点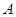 、
、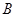 、
、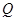 为切点作抛物线
为切点作抛物线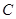 的三条切线
的三条切线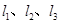 ,若
,若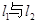 、
、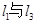 、
、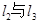 分别相交于D、E、H,设
分别相交于D、E、H,设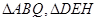 的面积依次为
的面积依次为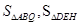 ,记
,记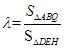 ,问:
,问: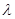 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。