已知线段AB，只用圆规找AB的中点P．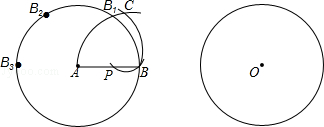
作法：
（1）以A为圆心，AB长为半径作圆；
（2）以B为圆心，AB长为半径在圆上连续截取，记截点为B1，B2，B3，B4，B5；
（3）以B3为圆心，BB3长为半径画弧；以B为圆心，AB长为半径画弧，与前弧交于点C；
（4）以C为圆心，CB长为半径画弧交线段AB于点P．
结论：点P就是所求作的线段AB的中点．
（1）配合图形，理解作法，根据作图过程给予证明：点P是线段AB的中点．
（2）已知⊙O，请只用圆规把圆周四等分．（保留作图痕迹，不要求写作法）
相关试题
÷
如图，已知
中，
，
，
，
是
边上的中点，
是
边上的点（不与端点重合），
是
边上的点，且
∥
，延长
与直线相交于点
，
点是延长线上的点，且
，联结
，设
，
.
（1）求
关于
的函数关系式及其定义域；
（2）联结
，当以
为半径的
和以为半径的
外切时，求
的正切值；
（3）当
与
相似时，求
的长.
的图像和二次函数
的图像都经过A、B两点，且点A在y轴上，B点的纵坐标为5. 
∥
时，求C点坐标.推荐套卷
粤公网安备 44130202000953号