为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
相关知识点
推荐套卷

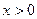 )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)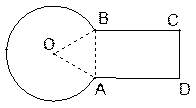


 中,
中,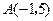 ,
, ,
, .
. 关于
关于 轴的对称图形
轴的对称图形 .
. 的坐标.
的坐标.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号