（本小题满分12分）如图，在四棱锥P﹣ABCD中，底面ABCD是梯形，PA⊥底面ABCD，其中BA⊥AD，AD∥BC， AC与BD交于点O，M是AB边上的点，且
，已知PA=AD=4，AB=3，BC=2．
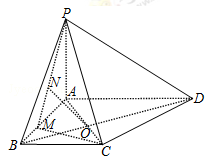
（Ⅰ）求平面PAD与平面PMC所成锐二面角的正切值；
（Ⅱ）已知N是PM上一点，且ON∥平面PCD，求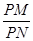
的值．
相关试题
．
，集合
,求
，
.
，当
时，对应
值的集合为
.
的值；（2）若
，求该函数的最值.
；
.
，
，
，
.
； （2）若
，求实数
的取值范围.
的圆
与
轴及直线
均相切，切点分别为
、
，另一圆
与圆
、
．
的平行线
，求直线推荐套卷
（本小题满分12分）如图，在四棱锥P﹣ABCD中，底面ABCD是梯形，PA⊥底面ABCD，其中BA⊥AD，AD∥BC， AC与BD交于点O，M是AB边上的点，且，已知PA=AD=4，AB=3，BC=2．
（Ⅰ）求平面PAD与平面PMC所成锐二面角的正切值；
（Ⅱ）已知N是PM上一点，且ON∥平面PCD，求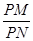的值．
粤公网安备 44130202000953号