小锋家有一块四边形形状的空地（如图，四边形ABCD），其中AD∥BC，BC=1.6m，AD=5.5m，CD=5.2m，∠C=90°，∠A=53°．小锋的爸爸想买一辆长4.9m，宽1.9m的汽车停放在这块空地上，让小锋算算是否可行．
小锋设计了两种方案，如图1和图2所示．
（1）请你通过计算说明小锋的两种设计方案是否合理；
（2）请你利用图3再设计一种有别于小锋的可行性方案，并说明理由．
（参考数据：sin53°=0.8，cos53°=0.6，tan53°=
）
相关试题
去年以来，我国中东部地区持续出现雾霾天气．我市某记者为了了解“雾霾天气的主要成因”，随机调查了部分市民，并对调查结果进行整理，绘制了如下尚不完整的统计表：
请根据图表中提供的信息解答下列问题：
（1）填空：m＝，n＝，扇形统计图中E组所占的百分比为；
（2）若该市人口约有75万人，请你估计其中持D组“观点”的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人持C组“观点”的概率是多少？
如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2．4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC约为多少米？（ sin42°≈0．7，tan42°≈0．9）
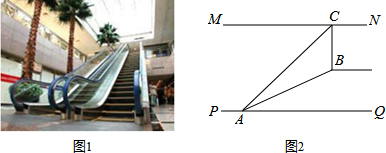
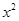+2x+2k－2=0有两个不相等的实数根．
，再选取一个合适的a值代入计算．
+
﹣sin45°
相关知识点
推荐套卷
粤公网安备 44130202000953号