一个容器中有一个进水管和两个出水管，从某一时刻开始2min内只进水不出水，在随后的4min内开启了一个出水管，既进水又出水，每个出水管每分钟出水7.5L，每分钟的进水量和出水量保持不变，容器内的水量y（L）与时间x（min）之间的函数关系如图所示．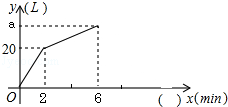
（1）求a的值；
（2）当2≤x≤6时，求y关于x的函数关系式；
（3）若在6min之后，两个出水管均开启，进水管关闭，请在图中补全函数图象．
相关试题
已知一次函数图象经过点(3 , 5) , (–4，–9)两点.求一次函数解析式.
求图象和坐标轴交点坐标.
求图象和坐标轴围成三角形面积.
点(a , 2)在图象上，求a的值.
某种拖拉机的油箱可储油40L，加满油并开始工作后，油箱中的余油量y（L）与工作时间x（h）之间为一次函数关系，如图所示．
求y与x的函数解析式．
一箱油可供拖位机工作几小时？
如图所示，
在正方形网格中，若点
的坐标为
，按要求回答下列问题：
在图中建立正确的平面直角坐标系；
根据所建立的坐标系，写出点
和点
的坐标；作出
关于
轴的对称图形
.(不用写作法)
中，
是
上一点，延长
到
，使
，连接
并延长交
于
．
；
绕点
顺时针旋转
得到
，
是什么特殊四边形？并说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号