国旗法对国旗的构成由明确的规定，国旗应为长方形，长与宽的比为3：2，某学校所使用的国旗正是按这一比例制作的，长为2.4m．已知学校的旗杆高为10m，在无风的天气里，国旗会自然下垂，求国旗下垂时最低处离地面的距离是多少？（结果保留一位小数，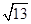
≈3.6）
相关试题
是等腰直角△
的直角边
上一点，
的垂直平分线
分别交
、
于点
、
、
，且
．当
时，试说明四边形
是菱形．
中，
6，
8，
平分∠
交
于点
，
平分∠
交
于点
．
为平行四边形；
中，点
是
的中点，且
⊥
．
的度数；
的长；
为一梯形纸片，
∥
，
．翻折纸片
与点
重合，折痕为
．已知
⊥
.
中，
∥
，
，
⊥
，延长
至点
，使
．
的度数．
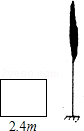
为等腰三角形．相关知识点
推荐套卷
国旗法对国旗的构成由明确的规定，国旗应为长方形，长与宽的比为3：2，某学校所使用的国旗正是按这一比例制作的，长为2.4m．已知学校的旗杆高为10m，在无风的天气里，国旗会自然下垂，求国旗下垂时最低处离地面的距离是多少？（结果保留一位小数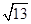，≈3.6）
粤公网安备 44130202000953号