在“五•一”期间,“佳佳”网店购进A、B两种品牌的服装进行销售,已知B种品牌服装的进价比A种品牌服装的进价每件高20元,2件A种品牌服装与3件B种品牌服装进价共560元.
(1)求购进A、B两种品牌服 装的单价;
(2)该网站拟以不超过11200元的总价购进这种两品牌服装共100件,并全部售出.其中A种品牌服装的售价为150元/件,B种品牌服装的售价为200元/件,该网站为了获取最大利润,应分别购进A、B两种品牌服装各多少件?所获取的最大利润是多少?
相关知识点
推荐套卷
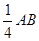 ,猜想EF与DE的位置关系,并说明理由.
,猜想EF与DE的位置关系,并说明理由.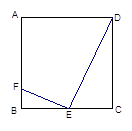
 中,
中,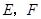 分别为边
分别为边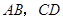 的中点,连接
的中点,连接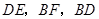 .
.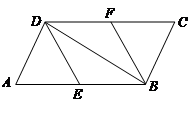
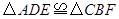 .
.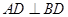 ,则四边形
,则四边形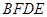 是什么特殊四边形?请证明你的结论.
是什么特殊四边形?请证明你的结论.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号