（本小题满分14分）设函数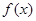
的定义域为R，当
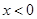时，
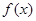
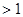，且对任意的实数
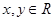，有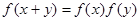
．
（1）求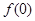
，判断并证明函数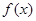的单调性；
（2）数列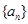
满足
，且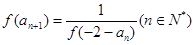
①求
的通项公式；
②当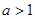
时，不等式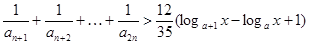
对不小于2的正整数
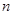恒成立，求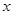
的取值范围．
的三视图.
推荐套卷
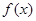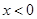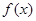
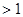（本小题满分14分）设函数的定义域为R，当时，，且对任意的实数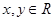，有．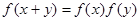
（1）求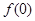，判断并证明函数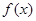的单调性；
（2）数列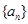满足，且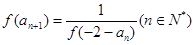
①求的通项公式；
②当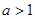时，不等式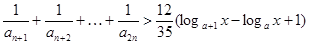对不小于2的正整数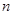恒成立，求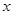的取值范围．
粤公网安备 44130202000953号